Heesch 28 Interlocking Tiles
Dutch artist M.C. Escher is famous for the images of a bird or a lizard that fits together with adjacent tiles without gaps. These tiles can extend to infinity on a surface. The essence of "Escher Tile" is that these are enclosures with one or two motifs.

I feel that the best mathematics to describe Escher tile is the set of 28 interlocking tiles published by Heinrich Heesch (1906-1995). Most people who studied this topic tends to use 17 Wallpaper groups to analyze the symmetry of the aggregate. There may be more than one way to look at this tiling. My friend Dr. Robert Fathauer said all tilings are patterns. But not all patterns are tilings. The 17 Wallpaper groups is best suited to study symmetry and pattern. The Escher Tile and the Heesch tiles are more related to tiles (finite enclosures). I hope the following two tables will show some of the differences.

Compare the two systems:

ICU Wallpaper	Heesch Tile Heinrich Heesch (1906-1995)
Properties of the aggregate	Dissection of tile boundary into lines and vertices
Each pattern has 1 to 4 properties	Each pair of line has one and only one property
All patterns have translation symmetry.	Only TT lines have translation symmetry.
A pattern may have no boundary and no limit on size.	A tile is composed of minimum 2 sets of lines. And a maximum of 4 sets of lines. A set is normally two separate lines from a symmetry movement. C line with half turn symmetry at center is a pair by itself. Half the boundary of the tile is a copy of the other half.
Patterns and images can fill the inside of a silhouette.	Inside of the tile is not part of the tile definition.
All p4 and p6 patterns have p2 property. Only smallest angle rotation is counted.	All line properties are counted. C lines (half turn) are counted with C3, C4 & C6.
Mirror and glide mirror lines have angle properties (parallel, intersect, 45 degree) and coincide (or not) with rotation centers	Lines on tile boundary cannot be mirrored. Glide mirror axes may be parallel or perpendicular.

When the pattern or tile has no mirror and no glide mirror property,
these are the different classifications:

ICU 17 Wallpaper Groups (Symmetry of Pattern)	Heesch 28 Basic Tiles (Symmetry of Line Components)	Escher example
p1	TTTT TTTTTT	Pegasus TTTT Sky and Water
p2	CCC CCCC TCCTCC TCTCC TCTC	Lizard TCTC Sea horse CCCC
p3	C3C3C3C3 C3C3C3C3C3C3	Escher Reptiles
p4	CC4C4 C4C4C4C4 CC4C4C4C4	Lizard C4C4C4C4
p6	CC6C6 CC3C3 C3C3C6C6 CC3C3C6C6	Dolphins CC3C3C6C6

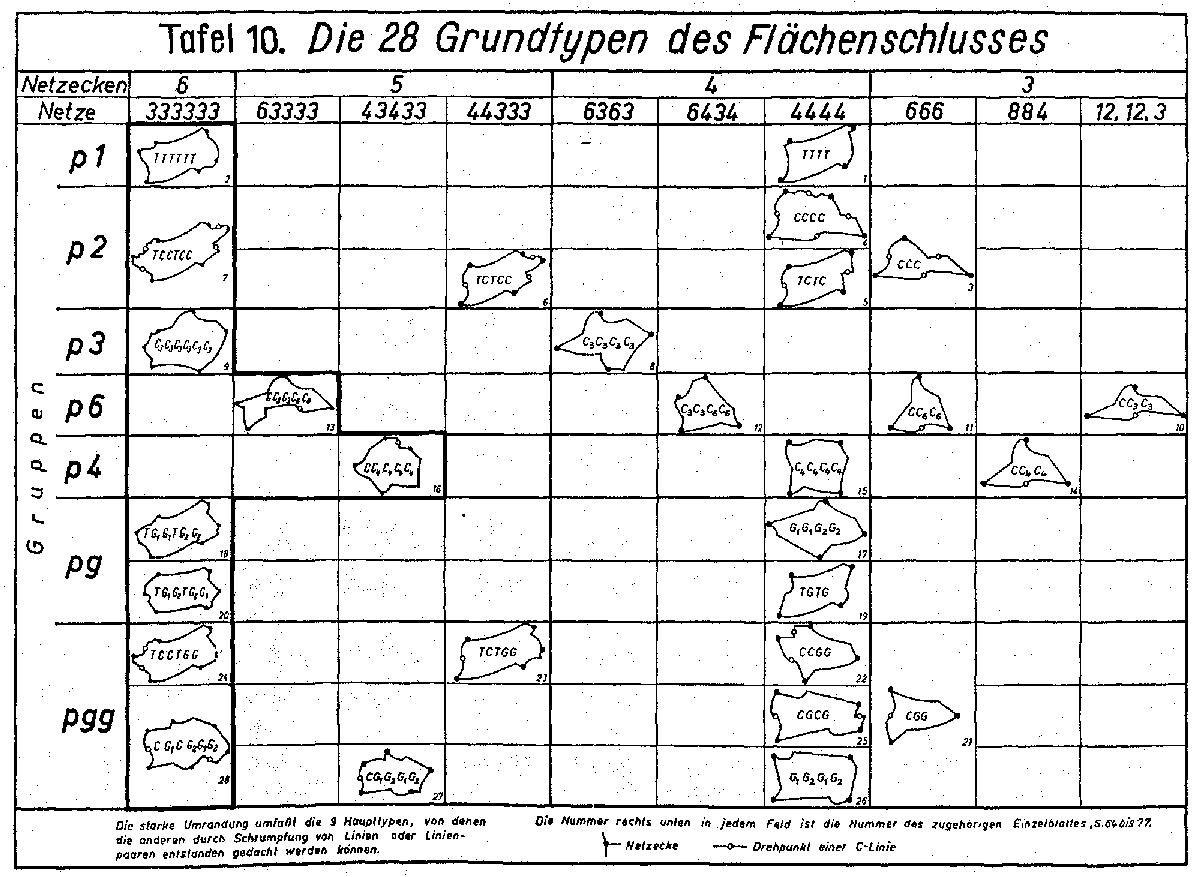
Heesch’s table of the 28 types of asymmetric isohedral tiles

Heesch's diagrams of the 28 types of interlocking shapes

Computer generated Escher tiles by William Chow 1979

Use of tessellations in art and product design 1980

Penrose tile in Architecture

Beautiful designs with mathematics ideas

Escher's lizards everywhere

Animated tiles by David Chow

My nephew Aaron Chow is 3D printer product designer

Screen shots of a CD to teach Tessellations

by William Chow October 17, 2007